Základní poznatky
Naleznete zde základní poznatky, užitečné pro řešení daných rovnic.
Absolutní hodnota
Absolutní hodnota je definována více způsoby. Pro počítání s ní se ovšem používají převážně dva. Jeden definuje absolutní hodnotu takto:
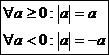
Druhý způsob ji definuje jako vzdálenost obrazu čísla na číselné ose od jejího počátku.
Pro absolutní hodnotu také platí tyto vzorce:
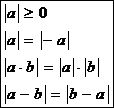
Druhá odmocnina
Druhou odmocninu budeme řešit jen pro Reálná čísla a tam je definována druhá odmocnina z x, takto:
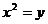
I pro druhou odmocninu si uvedeme několik platných vzorců:
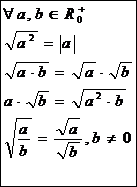
Úpravy při řešení rovnic
Řešení rovnice spočívá v nalezení všech čísel, která je možné dosadit za neznámou tak, aby platila rovnost. Každé takové číslo je tedy řešením rovnice, (jejím kořenem). Při hledání kořenů rovnice obvykle postupujeme tak, že místo dané rovnice píšeme nové tak, aby množina všech kořenů byla totožná. Úpravy, které toto splňují, se nazývají ekvivalentní.
Ekvivalentní úpravy
- Přičtení stejného výrazu obsahujícího neznámou (definovaného pro všechny hodnoty neznámé z množiny čísel, v níž rovnici řešíme) k oběma stranám rovnice
- Vynásobení obou stran rovnice stejným nenulovým číslem
- Ekvivalentní úpravy výrazů na jednotlivých stranách rovnice
Neekvivalentní úpravy
Jsou takové úpravy, které mění počet kořenů (navyšují ho). Tyto úpravy nazýváme neekvivalentní, nebo-li důsledkové. Takovou úpravu budeme potřebovat pouze jedinou
- Umocnění obou stran rovnice na druhou
Definiční obor
S řešením rovnic úzce souvisí i pojem definiční obor jednotlivých výrazů, které jsou v rovnici obsaženy. Definiční obor je množina čísel, pro která má daný výraz smysl (dělení nulou, druhá odmocnina ze záporného čísla).
