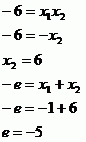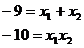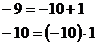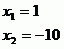Obecná kvadratická rovnice
Obecná kvadratická rovnice má tvar 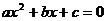 , kde
, kde 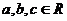 a zároveň platí
a zároveň platí 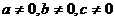 .
.
Tento typ kvadratické rovnice lze řešit dvěma způsoby. Jednak pomocí diskriminantu, což je metoda univerzální a lze ji tedy použít vždy. Také ji lze řešit pomocí Viètových vzorců, které vždy použít nelze, ale většinou je jejich užití rychlejší.
Řešení pomocí diskriminantu
Pokud máme rovnici ve tvaru 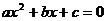 , pak pro výpočet diskriminantu D platí:
, pak pro výpočet diskriminantu D platí: 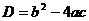 , kde
, kde 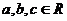 jsou koeficienty z obecné kvadratické rovnice.
jsou koeficienty z obecné kvadratické rovnice.
Nyní jsou možné dva případy. Buď 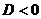 , pak kvadratická rovnice nemá v oboru Reálných čísel žádné řešení. Nebo
, pak kvadratická rovnice nemá v oboru Reálných čísel žádné řešení. Nebo  , pak má rovnice dvě řešení (pro
, pak má rovnice dvě řešení (pro 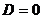 má jeden dvojnásobný kořen). Pro kořeny této rovnice platí:
má jeden dvojnásobný kořen). Pro kořeny této rovnice platí: 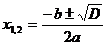 .
.

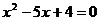
Nejprve spočítáme diskriminant. Po zjištění, že je nezáporný, dosadíme do vzorce a spočítáme oba kořeny.
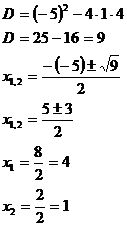
Řešení pomocí Viètových vzorců
Máme-li rovnici upravenou na tvar 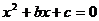 , pak pro kořeny rovnice (pokud existují) platí:
, pak pro kořeny rovnice (pokud existují) platí: 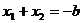 a
a 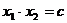
Tyto vztahy se nazývají Viètovými vzorci a práci s nimi si pro porovnání ukážeme na stejném příkladu, jako použití diskriminantu.

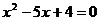
Hledáme dvě taková čísla  , která když sešteme, dostaneme číslo 5 a když je vynásobíme, získáme číslo 4.
, která když sešteme, dostaneme číslo 5 a když je vynásobíme, získáme číslo 4.

Je vcelku snadné uhádnout, že taková čísla jsou 1 a 4.
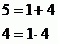
Tedy máme oba kořeny.
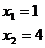
Řešené příklady
Ukážeme si několik řešených příkladů a bude-li to možné, tak oběma způsoby. Sami tak můžete posoudit, který způsob je v daném případě výhodnější.

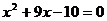
Nejprve spočteme diskriminant a poté použijeme vzorec.


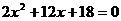
Pro tento způsob řešení je nutné nejdříve vydělit rovnici číslem 2, abychom před kvadratickým členem měli koeficient 1.
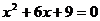
Nyní snadno uhádneme oba kořeny (v tomto případě jeden dvojnásobný).
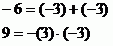
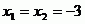
Nejprve rovnici vydělíme číslem 2, což sice není pro výpočet diskriminantu nezbytné, ale usnadní nám to pozdější počítání.
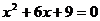
Nyní již spočteme kořeny pomocí diskriminantu.
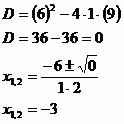


U této rovnice nám po vydělení číslem 2 nezůstanou všechny kořeny celočíselné. I tak lze Viètovy vzorce použít, ovšem nedá se to příliš doporučit, jelikož často jsou kořeny málo jednoduché na uhádnutí.
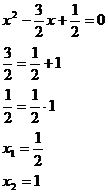
Dosadíme do vzorce pro diskriminant a vypočteme výsledky.
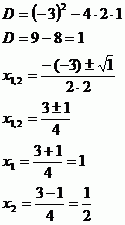

Pro tento příklad se Viètovy vzorce vůbec nehodí. Koeficienty nevycházejí celočíselné a tudíž by se kořeny velmi obtížně hádaly.
Pouze se dosadí do vzorce pro diskriminant
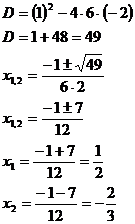

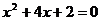
Příklad má celočíselné koeficienty a tedy vypadá, že lze touto metodou řešit. Po rozkladu však nelze kořeny uhodnout z hlavy a proto je lepší tento příklad řešit jinak.
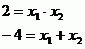
Pouze se dosadí do vzorce pro diskriminant.
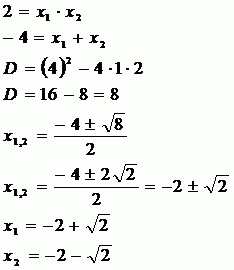

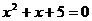
Nejde přímo o řešení pomocí Viètových vzorců, spíše o logickou úvahu. Platí totiž: 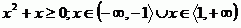 a tedy když připočteme ještě číslo 5, bude levá strana rovnice vždy kladná. Že rovnost nemůže platit ani pro zbylý interval je zžejmé. Z toho je vidět, že tato rovnice nemá v Reálných číslech žádné řešení.
a tedy když připočteme ještě číslo 5, bude levá strana rovnice vždy kladná. Že rovnost nemůže platit ani pro zbylý interval je zžejmé. Z toho je vidět, že tato rovnice nemá v Reálných číslech žádné řešení.
Dosadíme do vzorce pro diskriminant.
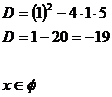
Jelikož je diskriminant záporný, rovnice nemá v Reálných číslech řešení.
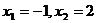
Každou kvadratickou rovnici, která má dva kořeny, lze zapsat ve tvaru: 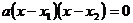 , stačí tedy takto kořeny zapsat a pak pokud platí
, stačí tedy takto kořeny zapsat a pak pokud platí 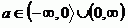 , máme všechny požadované kvadratické rovnice.
, máme všechny požadované kvadratické rovnice. 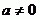 , protože by pak nešlo o kvadratickou rovnici.
, protože by pak nešlo o kvadratickou rovnici.
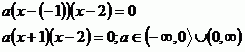
Rovnice by v obecném tvaru vypadala takto:  .
.
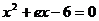 kořen
kořen 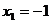
Pro zjištění druhého kořenu použijeme Viètovy vzorce a poté je použijeme ještě jednou pro vypočtení koeficientu e.