Rovnice s neznámou pod odmocninou
Tento typ rovnic se téměř vždy řeší umocněním obou stran rovnice na druhou. To je důsledková úprava ve chvíli, kdy nevíme, zda jsou všechny výrazy, které umocňujeme nezáporné. Pokud umocňujeme nezáporné výrazy, zkoušku dělat nemusíme. Pokud umocňujeme výrazy, o nichž nevíme, jestli jsou nezáporné, musíme zkoušku provést.
Obě metody jsou na čas podobně náročné, proto je spíše na řešiteli, která mu více vyhovuje.
Metoda umocnění s následným provedením zkoušky
Při řešení touto metodou rovnici obvykle nejdříve upravíme na takový tvar, abychom měli na jedné straně výraz s neznámou pod odmocninou a na druhé straně vše ostatní (i kdyby tam měl být další výraz s neznámou pod odmocninou). Následně umocníme obě strany na druhou, rovnici vyřešíme a provedeme zkoušku.
Tuto metodu si předvedeme na příkladu.
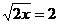
Rovnici máme v požadovaném tvaru, proto můžeme rovnou umocnit.
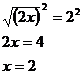
Máme tedy výsledek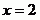 
, musíme ale zkontrolovat, zda je skutečně řešením rovnice a to pomocí zkoušky.
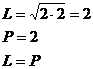
Levá strana se rovná pravé a proto 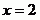je řešením zadané rovnice.
Metoda umocnění s určením definičního oboru
Pokud řešíme rovnici touto metodou, musíme si před umocněním zjistit, v jakém oboru jsou výrazy na obou stranách definovány. Jen drobné připomenutí: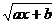 
má smysl, pokud platí 
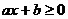. Jestliže si určíme definiční obor, ve kterém celou rovnici řešíme, budeme při umocňování zaručeně umocňovat nezáporné číslo a tedy půjde o úpravu ekvivalentní. Zkouška pak nebude nutná.
Ukážeme si tuto metodu na stejném příkladu.
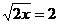
Nejprve si určíme pro jaká x má výraz pod odmocninou smysl.
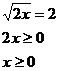
Výraz má smysl pro nezáporná x. Nyní je umocnění ekvivalentní úpravou (na levé straně jsme si zajistili, aby byla nezáporná a na pravé je číslo 2, které evidentně není záporné). Jen je nutné po získání výsledku zkontrolovat, zda do intervalu skutečně patří.
