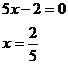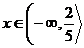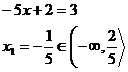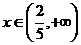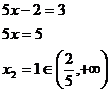Řešené příklady
V této části si ukážeme, jak řešit jednotlivé rovnice pomocí tří popsaných metod. Srovnáme si také, která metoda se na který typ příkladu hodí více a která méně. Metodou, která bude na řešení daného příkladu zcela nevhodná, se nebudeme zabývat vůbec. V závěru kapitoly bude ještě několik příkladů na procvičení těchto metod.
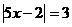
Nejprve musíme rovnici upravit, abychom měli vzdálenost bodu od x, nikoliv od 5x.
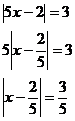
Hledáme tedy taková x, která mají od bodu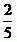 
vzdálenost 
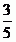. Taková x existují právě dvě.
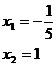
Zkontrolujeme, zda jsou obě strany nezáporné (jsou) a následně umocníme. Po umocnění upravíme vzniklou kvadratickou rovnici na obecný tvar a zkrátíme číslem 5.
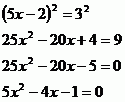
Vypočítáme diskriminant.
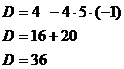
Nakonec spočítáme kořeny.
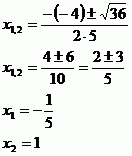
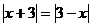
Zjistíme oba (podle počtu absolutních hodnot) nulové body a poté rozdělíme na tři případy.
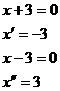
Vyřešíme pro každý interval zvlášť.
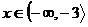
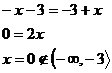
Výsledek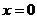 
nepatří do intervalu, ve kterém počítáme, proto rovnice nemá v tomto intervalu řešení.
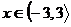
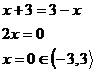
Zde 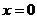do řešení patří, neboť je z intervalu, ve kterém počítáme.
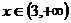
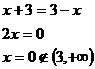
Opět vyjde 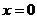, opět není z intervalu, pro který rovnici řešíme.
Výsledkem původní rovnice je množina všech výsledků, které jsme dostali z dílčích rovnic.
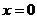
Pro tento příklad se bohužel nehodí.
Zkontrolujeme, zda jsou obě strany rovnice nezáporné a následně je umocníme. Po umocnění vyřešíme vzniklou (lineární) rovnici.
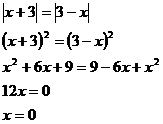
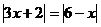
Zjistíme oba nulové body a poté rozdělíme na tři případy.
Vyřešíme pro každý interval zvlášť a následně zkontrolujeme, zda výsledek patří do intervalu.
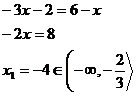
U druhého intervalu provedeme totéž.
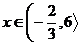
A ještě u třetího.
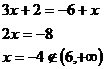
Kořeny původní rovnice tedy vypadají takto.
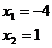
Nehodí se pro příklady, kde je více absolutních hodnot než jedna a kde se neznámá vyskytuje i mimo absolutní hodnotu.
Zkontrolujeme, zda jsou obě strany rovnice nezáporné a následně je umocníme. Po umocnění vyřešíme vzniklou kvadratickou rovnici.
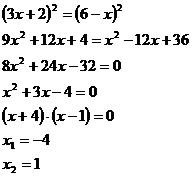
Zjistíme nulový bod.
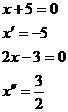
Vyřešíme pro každý interval zvlášť a následně vždy zkontrolujeme, zda výsledek patří do intervalu.
U tohoto intervalu je na první pohled patrné, že je pravá strana záporná a vzhledem k tomu, že má být zároveň levá strana nezáporná, řešení v tomto intervalu neexistuje.
Nyní druhý interval.
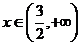
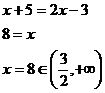
Kořenem původní rovnice je tedy jen tento.
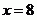
Nehodí se pro příklady, kde je více absolutních hodnot než jedna a kde se neznámá vyskytuje i mimo absolutní hodnotu.
Na podobné příklady se tato metoda příliš nehodí, ale ukážeme si, jak ji v podobném příkladu lze správně použít. Nejprve je pro umocnění potřeba zařídit, aby jedna strana nebyla záporná. Vzhledem k tomu, že levá strana rovnice je celá v absolutní hodnotě a tedy nezáporná, pravá musí být také nezáporná a podle toho určíme interval, pro který budeme řešit celou rovnici umocněním.
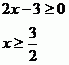
Poté řešíme v daném intervalu.
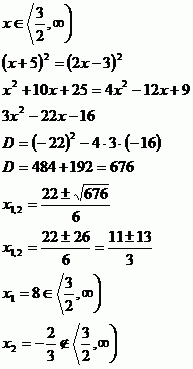
Dobře je na tomto příkladu vidět, že tato metoda skutečně není příliš vhodná pro podobné typy rovnic.
Zjistíme nulový bod a zároveň rovnou interval, pro který rovnici nemá smysl řešit (levá strana nezáporná, pravá záporná).
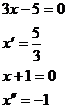
Vyřešíme pro každý interval zvlášť a následně vždy zkontrolujeme, zda výsledek patří do intervalu. Pro interval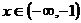
nemusíme řešit nic, neboť v něm nemá rovnice řešení. začneme proto druhým intervalem.
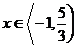
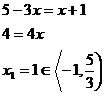
A ještě poslední interval.
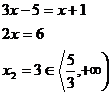
Výsledkem jsou tedy tyto dva kořeny zadané rovnice.
Nehodí se pro příklady, kde je více absolutních hodnot než jedna a kde se neznámá vyskytuje i mimo absolutní hodnotu.
Pro řešení takovéhoto příkladu není metoda vhodná, viz. příklad 4, kde je podrobnější vysvětlení a ukázka.
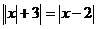
Nejprve si můžeme rovnici zjednodušit odstraněním jedné absolutní hodnoty. Stačí si všimnout, že je tam jedna zbytečná, neboť nic neovlivňuje.
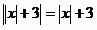
Budeme tedy řešit tuto rovnici.
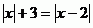
Spočteme nulové body.
A vyřešíme v jednotlivých intervalech.
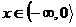
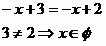
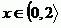
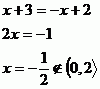
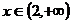
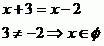
Zadaná rovnice nemá tedy řešení.
Nehodí se pro příklady, kde je více absolutních hodnot než jedna a kde se neznámá vyskytuje i mimo absolutní hodnotu.
Zkontrolujeme, že jsou obě strany nezáporné a umocníme. Nesmíme však zapomenout, že ve výrazu na levé straně nám jedna absolutní hodnota po umocnění zůstane.
Poté dořešíme metodou nulových bodů. Zjednodušili jsme ji touto úpravou o jeden interval. Nejprve tedy zjistíme nulové body.
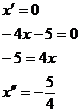
A následně rozdělíme na intervaly.
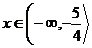
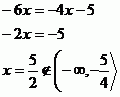
V tomto intervalu je pravá strana záporná, nemá tedy smysl v něm rovnici řešit.
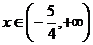
Zadaná rovnice nemá tedy řešení.
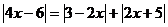
Nejprve si rovnici můžeme zjednodušit, když si všimneme, že absolutní hodnota vlevo je jen dvojnásobkem jedné z těch, které se vyskytují napravo. Můžeme tyto dva výrazy tedy od sebe odečíst.
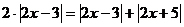
Budeme tedy řešit tuto rovnici.
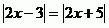
Spočteme nulové body.
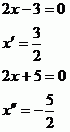
A vyřešíme v jednotlivých intervalech.
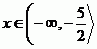
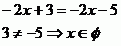
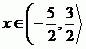
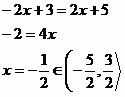
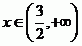
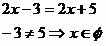
Řešení je tak pouze jedno.
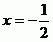
Nehodí se pro příklady, kde je více absolutních hodnot než jedna a kde se neznámá vyskytuje i mimo absolutní hodnotu.
Nejprve si rovnici můžeme zjednodušit, když si všimneme, že absolutní hodnota vlevo je jen dvojnásobkem jedné z těch, které se vyskytují napravo. Můžeme tyto dva výrazy tedy od sebe odečíst.
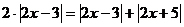
Budeme tedy řešit tuto rovnici.
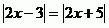
Nyní použijeme metodu umocnění.
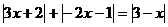
Nejprve určíme všechny nulové body
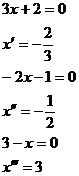
A postupně vyřešíme rovnici pro každý zvlášť.
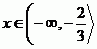
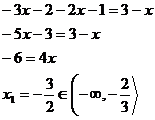
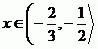
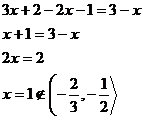
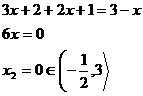
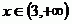
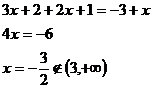
Celkově z toho vychází tyto kořeny.
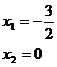
Nehodí se pro příklady, kde je více absolutních hodnot než jedna a kde se neznámá vyskytuje i mimo absolutní hodnotu.
Pro tento typ rovnice je metoda sice použitelná, ale velmi nevhodná a navíc stejně kombinovaná s metodou nulových bodů. Proto tu není toto řešení předvedeno.
