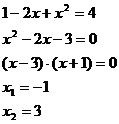Rovnice s absolutní hodnotou
Rovnice s absolutní hodnotou lze řešit třemi způsoby: Metodou nulových bodů, využitím geometrické představy a umocněním
Metoda nulových bodů
Při řešení touto metodou se postupuje tak, že se naleznou kořeny všech výrazů v absolutní hodnotě, které se v rovnici vyskytují. Tyto kořeny se nazývají nulové body. Poté rozdělíme interval, ve kterém jsme rovnici řešili původně, na několik vzájemně disjunktních intervalů, ohraničených získanými nulovými body a původními hranicemi intervalů tak, že při sjednocení všech intervalů dostaneme interval původní. Hranice (nulové body) vždy budou patřit do jednoho ze dvou intervalů, který určují.
Následně jen vyřešíme pro každý interval zvlášť a to tak, že odstraníme absolutní hodnoty (pokud jsme nulové body určili správně, můžeme vždy jednoznačně určit, zda je výraz v absolutní hodnotě kladný či záporný a díky tomu odstranit absolutní hodnotu). Na závěr vždy zkontrolujeme, zda výsledek, který jsme dostali, skutečně patří do intervalu, v němž jsme ho řešili. Množina všech takových výsledků je pak řešením rovnice.
Ukážeme si tuto metodu zvlášť na jednoduchém příkladu.
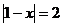
Nalezneme všechny nulové body (kdy jsou výrazy v absolutních hodnotách rovny 0).
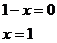
Získali jsme tedy dva intervaly, ve kterých budeme rovnici řešit.
-
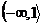
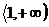
Nejprve tedy spočteme výsledek pro
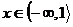
Jelikož je v tomto intervalu výraz uvnitř absolutní hodnoty kladný, pouze ji odstraníme a vyřešíme získanou lineární rovnici.
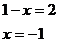
Nakonec zkontrolujeme, zda výsledek patří do intervalu, ve kterém řešíme.
-
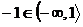
Pro druhý interval vyřešíme rovnici analogicky, tentokrát je výraz v absolutní hodnotě záporný a proto změníme znaménko a vyřešíme lineární rovnici. Opět je nutné zkontrolovat, zda výsledek patří do intervalu.
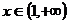
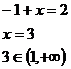
Nakonec jen zapíšeme všechna řešení dané rovnice.
Využití geometrické představy
Při použití této metody se využívá to, že vztah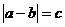 
znamená, že obraz čísla a je na číselné ose vzdálen od obrazu čísla b vzdálenost c.
Tento způsob řešení rovnic s absolutní hodnotou se hodí jen pro rovnice ve tvaru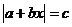 
, kde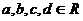 
. Nejlépe je to vidět na příkladu (pro srovnání použijeme stejný jako u předchozí metody).
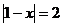
Víme tedy, že obraz čísla x je od obrazu čísla 1 vzdálen 2 jednotky.
Taková čísla jsou právě dvě, jedno napravo od 1 a druhé nalevo.
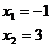
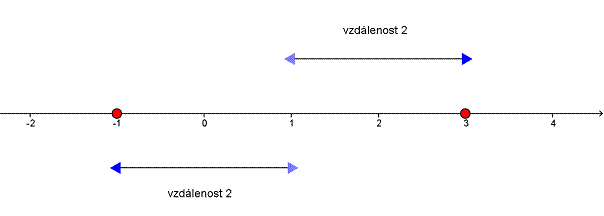
Pro lepší představu si to ukážeme ještě na obrázku:
Metoda umocnění rovnice
Tato metoda využívá především toho, že absolutní hodnota z libovolného výrazu je vždy nezáporná. V případě, že jsou obě strany nezáporné, můžeme je umocnit na druhou a poté řešit jako kvadratickou rovnici.
Nejlépe lze tato úprava použít v rovnicích, které je možné převést na tvar 
, kde 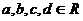a to především, pokud platí 
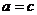, jelikož se odečte kvadratický člen a zbude lineární rovnice o jedné neznámé. Pro takové rovnice je tento způsob výpočtu asi nejrychlejší. Dá se ovšem použít i pro jiné typy rovnic s absolutní hodnotou, tam je ale rychlost výpočtu srovnatelná s metodou nulových bodů.
Ještě jednou si tedy ukážeme, jak vyřešit rovnici 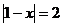, tentokrát za použití umocnění rovnice.
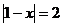
Zkontrolujeme, zda jsou obě strany rovnice nenulové (pokud ne, nelze tato metoda použít!) a pokud ano, umocníme je na druhou.
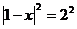
Převedli jsme na kvadratickou rovnici, kterou vyřešíme (pomocí Viètových vzorců).
